Natural Language Processing

  1. Introduction
  2. Recursive transition networks
  3. Generating sentences from a grammar
  4. Nested Networks
  5. Python generators
  6. Matching input sentences
  7. The match generator
  8. Retrieving the sentence structure
  9. Dealing with Ambiguity
  10. Parsing another language
  11. Practical considerations

Introduction

This is the first part of a multi-step project to parse and process small subsets of natural language. Here i part 1 we will explore the use of RTN's for representing grammars and Python code to both generate and parse sentences in a grammar. In part 2 we will match parsed sentences against a Knowledge base to perform sematic processing, that is, extract meaning from the sentence. Eventually, I hope to replicate Terry Winograd's Blocks World which will require sentence parsing, extraction of meaning, goal planning, and execution of instructions.

Keeping the code as simple as possible

Recursive transition networks

Recursive transition networks (RTN) are useful devices for representing grammars in both human and computer languages. The kind of grammars that can be represented with RTN's are called context-free. They consist of rules for how words may be put together into structures and, in turn, how those structures may be built into larger structures. For a particular grammar a valid sentence is a list of words that follow the rules of the grammar. We will use the word sentence with this more restricted meaning a lot.

The computer language Pascal (among others) is formally defined using RTN's.

Here is a very simple example. The grammar in figure 1 consists of a single sentence, the word red followed by the word book.

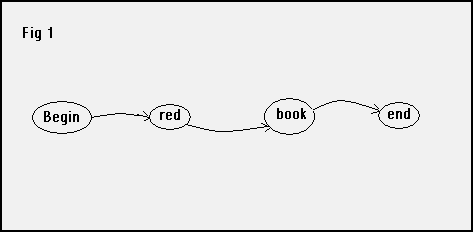
For our purposes an alternative, but equivalent, format is more useful because it is easily translated into a Python dictionary. The network that defines this sentence consists of nodes (1, 2, END) connected by named arcs. The name of an arc indicates what word(s) will carry us from one node to another, and in which direction. You traverse the network by starting at node 1 and finding a path to node END.

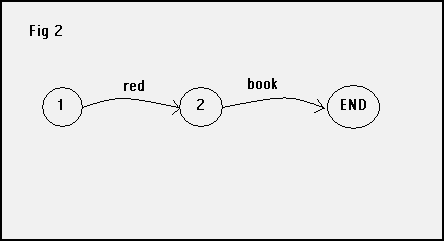
And here is one way to represent the network in Python

net1 = {
 'sentence': {
         1: (("red",  2),    ),
         2: (("book", END), )
         }
}

The network "sentence" refers to a dictionary whose entries are the states. Each state (1,2..) consists of a tuple of transitions where. The word "red" in state 1, for example, takes us to state 2. The "sentence" network is itself inside a dictionary of networks (net1). Now this is, momentarily, a bit more complex than it needs to be. But we're preparing the groundwork to have a family of networks working together.

So, the nodes in the network are key/value pairs in a dictionary. The key is the name of the node (1,2) and the value is a list of arcs. Each arc is a two valued tuple describing the word and destination. The END node does not need to be defined since no arcs emanate from it. END is simply a defined constant.

Let's move on to a somewhat more interesting grammar. Figure 3 describes a grammar that consists of the word book preceded by one or more words red. So red book and red red red book are both valid sentences in the grammar.

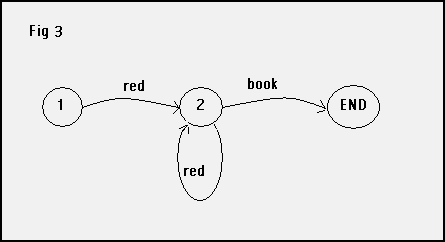
And here is the Python version.

net2 = {
 'sentence': {
         1: (("red", 2), ),
         2: (("red", 2), ("book", END))
         }
}

Generating sentences from a grammar

It's easy to write a python function that will generate a random sentence in a grammar. For our simple non-recursive grammars above the following function works well.

import random
END   = None 

def gen1(net) :
    "Generate random sentence from simple net. Non recursive"
 # p points to state 1 initially. s is the sentence being build
    p = net[1]; s = ""
    while 1 :
        choose = random.randrange(len(p)) # A random transition in this state
        s = s + " " + p[choose][0]        # The word on the arc
        next = p[choose][1]               # To the next state
        if next == END : return s
        p = net[next]

The variable p keeps track of the current node and s is the sentence as it is being built. From each node we choose an arc at random (line 8), add its word to the sentence (line 9) and advance to the next node (line 12). The sentence is returned when the END node is reached (line 11).

Let's play with this a bit. You can access code and grammar at rtn.py and simple.py

>>> import rtn
>>> import simple
>>> rtn.gen1(simple.net1['sentence'])
' red book'
>>> rtn.gen1(simple.net1['sentence'])
' red book'
>>> rtn.gen1(simple.net2['sentence'])
' red red red book'
>>> rtn.gen1(simple.net2['sentence'])
' red red book'

The network net1 always produces the same sentence, but net2 generates a random number of red words preceding book.

Nested Networks

The following assumes a rudimentary knowledge of english grammar. You need to at least know the difference between nouns, prepositions, verbs and adjectives. There are lots places to get this information.

Extending our simple networks to recursive networks requires just one change. Allow the label on an arc to reference either a word or another network. Here is an example of 3 simple networks article, noun1 and adjective along with a recursive network noun2. These 2nd order nouns are optionally preceded by the word the or a followed by zero or more adjectives.

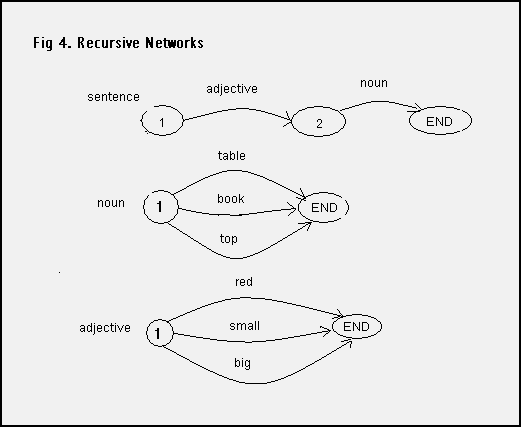
The recursive network net3 is defined in Python as you probably already suspect. The subnetworks are defined first. 

net3 = {
 'sentence': {
         1: (('adjective', 2), ),
         2: (('noun'  , END),  )
         },

 'noun'  : {
         1: (("book",END),("table",END),("top",END),("cover",END))
         },

 'adjective': {
         1: (("big",END),("small",END),("red",END))
         }
}

A small modification in the generator function is needed to make it work recursively.

def gen2(network, name) :
    "Generate random sentence, allow recursive network"
    net = network.get(name)
    if not net : return name     # terminal node
    p = net[1]; s = ""
    while 1 :
        choose = random.randrange(len(p))
        s = s + " " + gen2(network, p[choose][0])
        next = p[choose][1]
        if next == END : return s
        p = net[next]

Now the name passed to the function may be either a word or a subnetwork. The fourth line checks if it refers to a network and, if not, simply returns it. Otherwise line 8 calls gen2 recursively to expand the subnetwork. Let's generate some nouns, adjectives and sentences in our tiny grammar. 

>>> import rtn, simple
>>> rtn.gen2(simple.net3, "noun")
' table'
>>> rtn.gen2(simple.net3, "noun")
' top'
>>> rtn.gen2(simple.net3, "adjective")
' big'
>>> rtn.gen2(simple.net3, "adjective")
' small'
>>> rtn.gen2(simple.net3, "sentence")
'  big   table'
>>> rtn.gen2(simple.net3, "sentence")
'  red   book'
>>>

Now suppose that instead of generating a random sentence, we want to generate all possible sentences in a grammar. We can do this because our little grammar still finite.

But is there an easy way to generate all sentences in a grammar? This brings us to a new topic

Python generators

Generators are new to Python 2.2. You may think of them as functions that return multiple values one at a time to the caller, but maintaining their internal state (where they are and the value of local variables) between calls. They are very convenient when used with a for loop.

Here's a very simple example

>>> def gg() :
...     yield 2
...     yield 4
...     yield 8
...
>>> for i in gg() : print i
...
2
4
8
>>>

What turns a function definition into a generator is the use of the keyword yield which returns a value but keeps a bookmark of where it left off and retains values for local variables. The for loop will keep getting values from the generator until an explicit return in the generator is encountered or the generator falls off the end (an implicit return).

Generators are actually objects with a next method that is used by the for loop. A generator raises a specific exception when a return is excecuted, explicitly or implicitly.

Here is a generator that will generate all the sentences in the little recursive grammar above.

def gen3(network, label, state) :
    "Use generator to yield all possible sentences"
    if not network.get(label) : yield label  # if not a subnet stands for itself
    elif state == END         : yield ""     # no state. end of road
    else :
        net = network[label]
        p = net[state]; s = ""
        for labl,nextState in p :
            for word in gen3(network,labl,1) :
                for rest in gen3(network,label,nextState) :
                    yield word + " " + rest

This generator is doubly recursive and deserves a close study. When it is entered label may be subnetwork or a terminal word (like red). Basically, from a given state, each arc is tried. For each word (terminal or subnetwork) the arc label produces, we check from the target node to see if the END can be reached and yield the sentence accordingly. It is tricky.

Let's try this out.

>>> import simple
>>> import rtn
>>> for x in rtn.gen3(simple.net3,"noun",1) : print x
... 
book 
table 
top 
cover 
>>> for x in rtn.gen3(simple.net3,"adjective",1) : print x
... 
big 
small 
red 
>>> for x in rtn.gen3(simple.net3,"sentence",1) : print x
... 
big  book  
big  table  
big  top  
big  cover  
small  book  
small  table  
small  top  
small  cover  
red  book  
red  table  
red  top  
red  cover  
>>>

As an exercise, figure out why the words are separated by 2 spaces instead of 1.

Matching input sentences

Usually, we want to see if a given sentence is valid in the grammar and, if so, what are the constituent parts and how are they related to one another. Sometimes there are multiple possibilities. For example, with the sentence, The book on the table that is red, you can't tell whether it is the table or the book that is red. Of course we humans will rely on context for resolving ambiguities. In the sentence, The man wearing the hat that is green, it is almost certain that it is the hat that is green since you almost never see martians wearing hats. But computer programs cannot be expected to know such things. At least not yet! So if our grammar allows ambiguity, the matching algorithm should find multiple interpretations.

Our approach will be to generate all sentences that match an input sentence. If we are unable to find at least one match the sentence is not valid for our grammar. Later, as the match is generated we will track the structures built in subnetworks and combine them into nested list structures. The nesting will show the relationship of the parts in the same way that a sentence diagram does.

We are going to build a noun phrase grammar that includes prepositional phrases. Much like adjectives, these qualify (or zero in on) a noun. The book on the table with a red cover has two prepositional phrases both of which distinguish this book from, perhaps, others nearby. However, notice the ambiguity. Is the book or the table covered?

Let's look at a grammar that brings this together. You can access the code in english.py. Here it is.

#
#  e n g l i s h . p y
#
END = None

net = {
    ":noun1": {
        1: (("book",END),("table",END),("top",END),("cover",END))
        },

    ":article": {
        1: (("the",END),("a",END),("an",END))
        },

    ":adjective": {
        1: (("big",END),("small",END),("red",END))
        },

    ":preposition": {
        1: (("on",END),("of",END),("in",END),("with",END))
        },

    ":noun2": {
        1: ((":article", 1), ("",2)),
        2: ((":adjective", 2), (":noun1", END))
        },

    ":prepPhrase": {
        1: ((":preposition", 2), ),
        2: ((":noun3", END), )
        },

    ":noun3": {
        1: ((":noun2", END), (":noun2", 2)),
        2: ((":prepPhrase", END), (":prepPhrase", 2))
        },
}

Let's note a few things. The names of the networks now start with a ":". There are two reasons for this. One, we can immediately see that a word represents a subnetwork rather than itself. Two, it allows the name of a subnetwork to stand for itself. Using the colon is simply a convention. The code does not care.

So, here we have basic nouns (:noun1) like "book" and "table", modified nouns (:noun2) that include a possible article (the, a) and perhaps adjectives (red, big) and now noun phrases (noun3) that include prepositional phrases

Two special things need to be brought to attention. First, notice the ("",2) in state 1 in the :noun2 network. If an :article is not found, we basically can proceed to state2 for free, without consuming any input

Next, notice that in state 2 of :prepPhrase the noun inside the prepositional phrase is also a :noun3. That means, of course, that its noun can also be modified by its own prepositional phrase. We'll see the implications of that shortly.

The match generator

Our first match generator is very simliar to gen3 above.

def match1(network, label, state, input) :
    if   state == END : yield input[:]
    elif not input    : return
    elif not network.get(label) :
        if label == ""       : yield input[0:]  # free pass
        if label == input[0] : yield input[1:]
    else :
        net = network[label]
        p = net[state]; s = ""
        for labl,nextState in p :
            for input1 in match1(network,labl, 1, input) :
                for rest in match1 (network,label,nextState, input1) :
                    yield rest

Breathe deeply and relax. It's mostly the same code with the addition of "input" to be matched. The input consists of words in a list like "['the','big','red','book']". As possibilities are generated they must match the input and as that happens the REST of the input is yielded as a result. At the single word level this is "yield input[1:]" and at the phrase level this is "yield rest".

In line 5 (free pass) we are allowing an arc to jump from one state to another without consuming input. Basically an unlabeled arc. This will allow an article like "the" to be optional.

A subtle point should be noted. Yielding input[0:] and input[1:] create new lists in Python which will be independent of whatever else might happen to input. Lists are mutable objects and the program may, at any time, may be generating multiple matches. If these matches were all modifying a common list, they could easily get into the situation of stepping all over their own toes.

Let's play with this a bit. Notice that the words of our input are already split into a list and that a flag word "xx" is being appended.

>>> import english, rtn
>>> for s in rtn.match1(english.net, ':noun1', 1, ['book','xx']) : print s
['xx']

Here we have a simple match on the word book. It is consumed leaving 'xx' unmatched.

>>> for s in rtn.match1(english.net, ':noun1', 1, ['the','book','xx']) : print s
>>> for s in rtn.match1(english.net, ':noun2', 1, ['the','red','book','xx']) : print s
['xx']

Trying to match "the book" to a :noun1 fails, but a :noun2 can handle that along with an adjective "red".

Retrieving the sentence structure

Our match generator generates values containing the input that remains to be matched. We would also like to generate a data structure showing the sentence structure of the input that has been matched.

We'll generate nested tuples, one tuple for each network. An example should make this fairly clear. The noun2 sentence the red book is represented by the set of nested tuples

>>> for s in rtn.match2(english.net, ':noun2', 1, ['the','red','book','xx']) : print s
(['xx'], (':noun2', (':article', 'the'), (':adjective', 'red'), (':noun1', 'book')))

The remaining input "xx" is returned along with a parse tree, each node a 2 element tuple. The first element of each tuple contains the name of the network and the second is the subtree or node that satisfies it. This format makes it fairly easy to do semantic analysis.

And this is the python code:

def match2(network, label, state, input,ind=0) :
    if   state == END : yield input[:],None
    elif not input    : return
    elif not network.get(label) :
        if label == ""       : yield input[0:],label  # free pass
        if label == input[0] : yield input[1:],label
    else :
        net = network[label]
        p = net[state]; s = ""
        trace = [label]
        for labl,nextState in p :
            sav1 = trace[:]
            for input1,trace1 in match2(network,labl,1,input) :
                if trace1 : trace.append(trace1)
                sav2 = trace[:]
                for rest,trace2 in match2(network,label,nextState,input1) :
                    if trace2 : trace = trace + list(trace2[1:])
                    yield rest, tuple(trace[:])
                    trace = sav2[:]
                trace = sav1[:]

This is essentially match1 extended to generate trace tuples. At each level a different trace is started at line 10, grown at line 14 when the first arc is traversed and the rest of it gathered at line 17. The appends and additions are then backed off in lines 19 and 20 in order not to corrupt further possibilities. Incidentally, Don't feel bad if you have to study this closely. I spent hours getting this to work correctly.

Finally, our third matching function is very simple. It generates solutions only where the complete input is matched. It simply yields the trace.

def match3 (network, label, state, input) :
    "Use generator to yield all possible matching sentences that consume input"
    import string
    for input,trace in match2(network, label, state, input) :
        if not input : yield trace

Dealing with Ambiguity

Let's now play with a sentences that lead into ambiguity.

>>> import rtn, english
>>> sentence = ['a','book','on','the','table']
>>> for t in rtn.match3(english.net, ':noun3', 1, sentence) : print "Got one!!", t
Got one!! (':noun3', (':noun2', (':article', 'a'), 
             (':noun1', 'book')), (':prepPhrase', 
                (':preposition', 'on'), (':noun3', 
                  (':noun2', (':article', 'the'), (':noun1', 'table')))))
>>>

That's straightforward. I fussed with the indentation on the trace tree to make it more readable. But now notice this variation.

>>> sentence = ['a','book','on','the','table','with','a','cover']
>>> for t in rtn.match3(english.net, ':noun3', 1, sentence) : print "Got one!!", t
... 
Got one!! (':noun3', (':noun2', (':article', 'a'), 
            (':noun1', 'book')), (':prepPhrase', 
               (':preposition', 'on'), (':noun3', 
                   (':noun2', (':article', 'the'), (':noun1', 'table')), 
                     (':prepPhrase', (':preposition', 'with'), (':noun3', 
                        (':noun2', (':article', 'a'), (':noun1', 'cover')))))))

Got one!! (':noun3', (':noun2', (':article', 'a'), 
            (':noun1', 'book')), (':prepPhrase', 
               (':preposition', 'on'), (':noun3', 
                   (':noun2', (':article', 'the'), (':noun1', 'table')))),
           (':prepPhrase', (':preposition', 'with'), (':noun3', 
              (':noun2', (':article', 'a'), (':noun1', 'cover')))))
>>>

Do you see the difference? In the first interpretation, "with a cover" applies to to the table. In the second, it is the book that has a cover. It's all in counting the parans.

Parsing another language

Finally, let's contrast an english phrase with a japanese one and create a little RTN grammar for japanese.

The phrase we will parse is in english the book on top of the table.

Now in japanese there are no articles (the, a, an). Prepositional phrases precede the noun and the preposition itself comes at the end. So the sentence looks like the following

taberu   no   ue   ni  hon
table    of   top  on  book

See japanese.py for the networks.

>>> import japanese
>>> sentence = ["taberu","no","ue","ni","hon"]
>>> for t in rtn.match3(japanese.net, ':noun3', 1, sentence) : print "Got one!!", t
Got one!! (':noun3', (':prepPhrase', (':noun2', (':noun1', 'taberu')), 
            (':preposition', 'no')), (':prepPhrase', (':noun2', (':noun1', 'ue')), 
            (':preposition', 'ni')), (':noun2', (':noun1', 'hon')))
>>>

Practical considerations

We just used a network for lexicons of nouns, adjectives, etc. but this would be impractical for anything other than the toy grammars shown here. Instead, having :noun1 be a network of individual words it would be more practical to have it call a function that accesses a lexicon with a structure indicating a number of things about the word, including that it is a noun and its japanese translation is taberu. Of course, table can also be a verb in which case it would have a different a second lexicon entry

In the next section (late 2009) we'll add the ability to have function calls inside the network. This will make it possible to extend program in interesting ways. We'll also start to play with the semantics of our input sentences, extracting meaning. Keep in touch.

Index