5. Funciones productivas¶

5.1. Valores de retorno¶

Las funciones de biblioteca que hemos usado, como abs, pow, y max han producido resultados. Llamar a cada una de estas funciones genera un nuevo valor, que usualmente asignamos a una variable o usamos como parte de una expresión.

el_mayor = max(3, 7, 2, 5)
x = abs(3 - 11) + 10

Pero hasta ahora ninguna de las funciones que hemos escrito ha devuelto un valor.

En este capítulo escribiremos funciones que devuelvan valores, que llamaremos funciones productivas, a falta de un nombre mejor. El primer ejemplo es area, que devuelve el área de un círculo con un radio dado:

def area(radio):
    temporal = 3.14159 * radio**2
    return temporal

Ya hemos visto antes la sentencia return, pero en una función productiva la sentencia return incluye un valor de retorno. Esta sentencia significa: “Retorne inmediatemente de esta función y use la siguiente expresión como un valor de retorno”. La expresión dada puede ser arbitrariamente complicada; así pues, podríamos haber escrito esta función más concisamente:

def area(radio):
    return 3.14159 * radio**2

Por otra parte, las variables temporales como temporal suelen hacer más fácil la depuración.

A veces es útil tener múltiples sentencias de retorno, una en cada rama de una sentencia condicional. Ya hemos visto la función de biblioteca abs, ahora veamos cómo escribir nuestra propia función de valor absoluto:

def valor_absoluto(x):
    if x < 0:
        return -x
    else:
        return x

Puesto que estas sentencias return están en una condicional alternativa, sólo se ejecutará una de ellas. En cuanto se ejecuta una de ellas, la función termina sin ejecutar ninguna de las sentencias siguientes.

Otra forma de escribir la función anterior es omitir else y sólo agregar después de la condición if una segunda sentencia return.

def valor_absoluto(x):
    if x < 0:
        return -x
    return x

Piense en esta versión y convénzase que funciona igual que la primera.

El código que aparezca después de la sentencia return, o en cualquier otro lugar al que el flujo de ejecución nunca llegará, se llama código muerto.

En una función productiva es una buena idea asegurarse que cualquier posible recorrido del programa llegue a una sentencia return. La siguiente versión de la función valor_absoluto falla en este cometido:

def valor_absoluto(x):
    if x < 0:
        return -x
    elif x > 0:
        return x

Esta versión no es correcta porque si sucede que x es igual a 0, ninguna de las condiciones es verdadera, y la función termina sin alcanzar una sentencia return. En este caso, el valor de retorno es un valor especial llamado None:

>>> print valor_absoluto(0)
None

None es el único valor de un tipo llamado NoneType:

>>> type(None)
<type 'NoneType'>

Todas las funciones de Python retornan None siempre que no devuelvan otro valor.

5.2. Desarrollo de programas¶

En este punto usted debería ser capaz de leer funciones completas y deducir lo que hacen. También, si ha estado haciendo los ejercicios, ya ha escrito algunas funciones pequeñas. Conforme vaya escribiendo funciones más extensas puede empezar a tener mayores dificultades, especialmente con errores en tiempo de ejecución y semánticos.

Para lidiar con programas de complejidad creciente, vamos a sugerirle una técnica llamada desarrollo incremental. El objetivo del desarrollo incremental es evitar largas sesiones de depuración, adicionando y probando solamente pequeñas porciones de código cada vez.

Por ejemplo, suponga que desea encontrar la distancia entre dos puntos dados por las coordenadas (x₁, y₁) y (x₂, y₂). Por el teorema de Pitágoras, la distancia es:

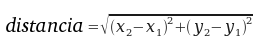
El primer paso es considerar qué aspecto tendría la función distancia en Python. En otras palabras, ¿cuáles son las entradas (parámetros) y cuál es la salida (valor de retorno)?

En este caso los dos puntos son las entradas, que podemos representar usando cuatro parámetros. El valor devuelto es la distancia, que es un valor de punto flotante.

Ya podemos escribir una primera versión de la función:

def distancia(x1, y1, x2, y2):
    return 0.0

Obviamente esta versión de la función no calcula distancias; siempre devuelve cero. Pero es correcta sintácticamente y se ejecutará, lo que implica que la podemos probar antes de que la hagamos más compleja.

Para probar la nueva función la llamamos con una muestra de valores:

>>> distancia(1, 2, 4, 6)
0.0

Elegimos estos valores de tal forma que la distancia horizontal sea igual a 3 y la distancia vertical sea igual a 4; de esa manera el resultado es 5 (la hipotenusa del triángulo 3-4-5). Cuando se comprueba una función, es útil conocer la respuesta correcta.

Hasta el momento hemos confirmado que la función es sintácticamente correcta, por lo que podemos empezar a agregar líneas de código. Después de cada cambio incremental, probamos de nuevo la función. Si ocurre un error, sabemos donde debe estar — en la última línea que agregamos.

El paso lógico siguiente en el cálculo es encontrar las diferencias x₂ - x₁y y₂ - y₁. Almacenaremos estos valores en variables temporales llamadas dx y dy y los mostraremos.

def distancia(x1, y1, x2, y2):
    dx = x2 - x1
    dy = y2 - y1
    print "dx es", dx
    print "dy es", dy
    return 0.0

Si la función trabaja bien, las salidas deben ser 3 y 4. Si es así, sabemos que la función está obteniendo los parámetros correctos y realizando el primer cálculo correctamente. Si no, entonces sólo hay unas pocas líneas que revisar.

Enseguida calculamos la suma de los cuadrados de dx y dy:

def distancia(x1, y1, x2, y2):
    dx = x2 - x1
    dy = y2 - y1
    dalcuadrado = dx**2 + dy**2
    print "dalcuadrado es: ", dalcuadrado
    return 0.0

Note que hemos eliminado las sentencias print que escribimos en el paso anterior. El código eliminado se llama andamiaje porque es útil para construir el programa pero no es parte del producto final.

De nuevo querremos ejecutar el programa en esta etapa y comprobar la salida (que debería ser 25).

Finalmente, utilizando el exponente decimal 0.5 para encontrar la raíz cuadrada, calculamos y devolvemos el resultado:

def distancia(x1, y1, x2, y2):
    dx = x2 - x1
    dy = y2 - y1
    dalcuadrado = dx**2 + dy**2
    resultado = dalcuadrado**0.5
    return resultado

Si esto funciona correctamente, usted ha terminado. Si no, podría querer mostrar el valor de la variable resultado antes de la sentencia de retorno.

Al principio, debería añadir solamente una o dos líneas de código cada vez. Conforme vaya ganando experiencia, puede que se encuentre escribiendo y depurando trozos mayores de código. Sin embargo, el proceso de desarrollo incremental puede ahorrarle mucho tiempo de depuración.

Los aspectos clave del proceso son:

Inicie con un programa que funcione y hágale pequeños cambios incrementales. En cualquier momento, si hay un error, sabrá exactamente dónde está.
Use variables temporales para guardar valores intermedios para que pueda mostrarlos y verificarlos.
Una vez que el programa está funcionando, tal vez prefiera eliminar parte del andamiaje o consolidar múltiples sentencias en expresiones compuestas, pero sólo si eso no hace que el programa sea difícil de leer.

5.3. Composición¶

Ahora, como usted esperaría, se puede llamar a una función desde otra. Esta habilidad se llama composición.

Como ejemplo, escribiremos una función que tome dos puntos, el centro del círculo y un punto del perímetro, y calcule el área del círculo.

Suponga que el punto central está almacenado en las variables xc y yc, y que el punto del perímetro lo está en xp y yp. El primer paso es hallar el radio del círculo, que es la distancia entre los dos puntos. Afortunadamente hemos escrito una función, distancia, que realiza esta tarea, por lo que ahora todo lo que tenemos que hacer es usarla:

radio = distancia(xc, yc, xp, yp)

El segundo paso es encontrar el área del círculo usando este radio y devolver el resultado. De nuevo usaremos una de nuestras funciones definidas previamente:

resultado = area(radio)
return resultado

Envolviendo todo en una función, obtenemos:

def area2(xc, yc, xp, yp):
    radio = distancia(xc, yc, xp, yp)
    resultado = area(radio)
    return resultado

Hemos llamado a esta función area2 para distinguirla de la función area definida previamente. Sólo puede haber una única función con un determinado nombre dentro de un módulo.

Las variables temporales radio y resultado son útiles para el desarrollo y la depuración, pero una vez que el programa está funcionando, podemos hacerlo más conciso componiendo las llamadas a función:

def area2(xc, yc, xp, yp):
    return area(distancia(xc, yc, xp, yp))

5.4. Funciones booleanas¶

Las funciones pueden devolver valores booleanos, lo que a menudo es conveniente para ocultar complicadas comprobaciones dentro de funciones. Por ejemplo:

def es_divisible(x, y):
    if x % y == 0:
        return True
    else:
        return False

El nombre de esta función es es_divisible. Es común dar a las funciones booleanas nombres que suenan como preguntas que tienen como respuesta un si ó un no. La función es_divisible devuelve True o False para indicar si x es o no divisible por y.

Podemos hacer la función más concisa aprovechándonos del hecho de que la condición dentro de una sentencia if es en sí una expresión booleana. Podemos devolver el resultado directamente, evitando completamente la sentencia if:

def es_divisible(x, y):
    return x % y == 0

La siguiente sesión muestra la nueva función en acción:

>>> es_divisible(6, 4)
False
>>> es_divisible(6, 3)
True

Las funciones booleanas se usan a menudo en las sentencias condicionales:

if es_divisible(x, y):
    print "x es divisible entre y"
else:
    print "x no es divisible entre y"

Puede parecer tentador escribir algo como:

if es_divisible(x, y) == True:

Pero la comparación extra es innecesaria.

El tipo function

En Python, adicional a los tipos int, float, str, bool, y NoneType, tenemos el tipo function.

>>> def func():
...    return "la función func fue llamada..."
...
>>> type(func)
<type 'function'>
>>>

Así como otros tipos, las funciones se pueden pasar como argumentos a otras funciones:

def f(n):
    return 3*n - 6

def g(n):
    return 5*n + 2

def h(n):
    return -2*n + 17

def hazesto(valor, func):
    return func(valor)

print hazesto(7, f)
print hazesto(7, g)
print hazesto(7, h)

La función hazesto es llamada tres veces. El número 7 es el valor del argumento en cada llamada, y las funciones f, g y h se transmiten a su vez a través de func. La salida de este guión es:

15
37
3

Este ejemplo es un poco artificial, pero más adelante veremos situaciones donde es bastante útil pasar una función a otra función.

5.5. Programando con estilo¶

La facilidad de lectura de un programa es muy importante para los programadores, puesto que en la práctica la lectura y modificación de los programas requiere mucho más tiempo que el tiempo que se emplea en su escritura. Todos los ejemplos de este libro serán consistentes con la Python Enhancement Proposal 8 - Propuesta 8 de Mejoramiento de Python (PEP 8), que es una guía de estilo desarrollada por la comunidad Python.

Nota del traductor: Una traducción de la guía PEP 8 actualizada a agosto de 2007 se puede encontrar en PEP 8 en español.

Tendremos más que decir del estilo conforme nuestros programas sean más complejos, pero algunos puntos son de utilidad desde ahora:

use 4 espacios para el sangrado
las importaciones deberían estar en el inicio del archivo
separe las definiciones de función con dos líneas en blanco
mantenga juntas las definiciones de función
mantenga juntas al final del programa las sentencia de alto nivel — incluyendo las llamadas a función

5.6. Cadenas con comillas triples¶

Adicionalmente a las cadenas con comillas sencillas y dobles que vimos en Valores y tipos, Python también tiene cadenas con comillas triples:

>>> type("""Esta es una cadena con comillas triples usando 3 comillas dobles.""")
<type 'str'>
>>> type('''Esta es una cadena con comillas triples que usa 3 comillas sencillas.''')
<type 'str'>
>>>

Las cadenas con comillas triples pueden contener tanto las comillas sencillas como las dobles:

>>> print '''"Oh no", exclamó ella, "¡La bicicleta de Benito está quebrada!"'''
"Oh no", exclamó ella, "¡La bicicleta de Benito está quebrada!"
>>>

Finalmente, las cadenas con comillas triples pueden extenderse en varias líneas:

>>> mensaje = """Este mensaje podrá
... extenderse en varias
... líneas."""
>>> print mensaje
Este mensaje podrá
extenderse en varias
líneas.
>>>

5.7. Prueba unitaria con `doctest`¶

En el desarrollo de software en estos días es una buena práctica incluir una prueba unitaria automática del código fuente. La prueba unitaria provee una forma de verificar automáticamente que las piezas individuales del código, como las funciones, están trabajando apropiadamente. Esto hace posible cambiar, tiempo después, la implementación de una función y rápidamente probar que todavía hace lo que se supone que hace.

Python tiene en su biblioteca interna el módulo doctest para facilitar la prueba unitaria. El código para la prueba unitaria se puede escribir en una cadena con comillas triples en la primera línea del cuerpo de una función o guión. El código consiste en muestras de sesiones del intérprete de Python con una serie de entradas en el indicador de Python seguidas de las salidas esperadas del intérprete de Python.

El módulo doctest automáticamente ejecuta cualquier sentencia que inicie con >>> y compara la línea que sigue con la salida del intérprete.

Para ver cómo funciona, coloque lo siguiente en un guión que se llame misfunciones.py:

def es_divisible_entre_2_o_5(n):
    """
      >>> es_divisible_entre_2_o_5(8)
      True
    """

if __name__ == '__main__':
    import doctest
    doctest.testmod()

Las últimas tres líneas son para hacer que se ejecute el módulo doctest. Colóquelas al final de cualquier archivo que incluya código para prueba unitaria. En el Capítulo 10, donde trataremos el tema de módulos, explicaremos cómo funcionan estas instrucciones.

La ejecución del guión producirá la siguiente salida:

$ python misfunciones.py
**********************************************************************
File "misfunciones.py", line 3, in __main__.es_divisible_entre_2_o_5
Failed example:
    es_divisible_entre_2_o_5(8)
Expected:
    True
Got nothing
**********************************************************************
1 items had failures:
   1 of   1 in __main__.es_divisible_entre_2_o_5
***Test Failed*** 1 failures.
$

Este es un ejemplo de una <em>prueba fallida</em>. La prueba dice: si usted llama a la función es_divisible_entre_2_o_5(8) el resultado debería ser True. Puesto que como está escrita la función es_divisible_entre_2_o_5(8) no devuelve valor alguno, la prueba falla, y el módulo doctest nos dice que él esperaba el valor True, pero no obtuvo nada.

Podemos hacer que esta prueba pase devolviendo el valor True:

def es_divisible_entre_2_o_5(n):
    """
      >>> es_divisible_entre_2_o_5(8)
      True
    """
    return True

if __name__ == '__main__':
    import doctest
    doctest.testmod()

Si ejecutamos esto ahora no obtendremos salida alguna, lo que indica que la prueba pasó. Observe de nuevo que el código para la prueba unitaria debe estar ubicado inmediatamente después del encabezado de la definición de función con el fin de que pueda ser ejecutado.

Para ver más detalles de la salida, llame el guión con la opción -v en la línea de comandos:

$ python misfunciones.py -v
Trying:
    es_divisible_entre_2_o_5(8)
Expecting:
    True
ok
1 items had no tests:
    __main__
1 items passed all tests:
   1 tests in __main__.es_divisible_entre_2_o_5
1 tests in 2 items.
1 passed and 0 failed.
Test passed.
$

Aunque se pasó la prueba, nuestros casos de prueba son claramente inadecuados, puesto que es_divisible_entre_2_o_5 devolverá ahora el valor True no importando qué argumento se pase a la función. Aquí está la versión completa con casos de prueba más completos y con el código que hace que se pase la prueba:

def es_divisible_entre_2_o_5(n):
    """
      >>> es_divisible_entre_2_o_5(8)
      True
      >>> es_divisible_entre_2_o_5(7)
      False
      >>> es_divisible_entre_2_o_5(5)
      True
      >>> es_divisible_entre_2_o_5(9)
      False
    """
    return n % 2 == 0 or n % 5 == 0

if __name__ == '__main__':
    import doctest
    doctest.testmod()

Ahora ejecute este guión con la opción -v en la línea de comandos y observe lo que obtiene.

5.8. Glosario¶

función productiva: Función que devuelve un valor de retorno.
valor de retorno: Valor obtenido como resultado de una llamada a función.
variable temporal: variable usada para almacenar un valor intermedio en un cálculo complejo.
código muerto: Parte de un programa que nunca puede ser ejecutado, a menudo porque aparece después de una sentencia return.
None: Valor especial de Python que es devuelto por funciones que no tienen la sentencia return o la tienen sin argumento. El valor None es el único valor del tipo NoneType.
desarrollo incremental:: Plan de desarrollo de un programa que intenta evitar la depuración agregando y probando solamente una pequeña porción de código a la vez.
andamiaje:: Código que se usa durante el desarrollo de un programa pero que no es parte de la versión final del mismo.
función booleana:: Una función que devuelve un valor booleano.
composición (de funciones):: Llamar una función desde el cuerpo de otra, o usar el valor de retorno de una función como un argumento para llamar a otra.
prueba unitaria:: Procedimiento automático utilizado para validar que las unidades de código individuales funcionan correctamente. Python tiene el módulo doctest en su biblioteca para este propósito.

5.9. Ejercicios¶

Todos los ejercicios siguientes deberían agregarse a una archivo llamado cap05.py que contenga las siguientes líneas al final del archivo:

if __name__ == '__main__':
    import doctest
    doctest.testmod()

Después de completar cada ejercicio ejecute el programa para confirmar que pase la prueba unitaria de cada nueva función.

Escriba la función comparar que devuelva 1 si a > b, 0 si a == b, y -1 si a < b

def comparar(a, b):
    """
      >>> comparar(5, 4)
      1
      >>> comparar(7, 7)
      0
      >>> comparar(2, 3)
      -1
      >>> comparar(42, 1)
      1
    """
    #  El cuerpo de su función debería empezar aquí.

Complete el cuerpo de la función de forma tal que el código pase la prueba unitaria.

Use el desarrollo incremental para escribir una función llamada hipotenusa que devuelva la longitud de la hipotenusa de un triángulo rectángulo dadas las longitudes de los dos lados como parámetros. Guarde cada etapa del proceso de desarrollo incremental conforme lo vaya realizando.
```
def hipotenusa(a, b):
    """
      >>> hipotenusa(3, 4)
      5.0
      >>> hipotenusa(12, 5)
      13.0
      >>> hipotenusa(7, 24)
      25.0
      >>> hipotenusa(9, 12)
      15.0
    """
```
Cuando haya terminado, agregue su función completa, incluyendo el código para la prueba unitaria, al archivo cap05.py y confirme que el código pasa la prueba unitaria.

Escriba la función pendiente(x1, y1, x2, y2) que devuelva la pendiente de una línea que pasa por los puntos (x1, y1) y (x2, y2). Asegúrese que su implementación de la función pendiente puede pasar el siguiente código de la prueba unitaria:

def pendiente(x1, y1, x2, y2):
    """
      >>> pendiente(5, 3, 4, 2)
      1.0
      >>> pendiente(1, 2, 3, 2)
      0.0
      >>> pendiente(1, 2, 3, 3)
      0.5
      >>> pendiente(2, 4, 1, 2)
      2.0
    """

Ahora llame a la función pendiente en una nueva función llamada intercepcion(x1, y1, x2, y2) que devuelva la intersección de y de la línea que pasa por los puntos (x1, y1) y (x2, y2).

def intercepcion(x1, y1, x2, y2):
    """
      >>> intercepcion(1, 6, 3, 12)
      3.0
      >>> intercepcion(6, 1, 1, 6)
      7.0
      >>> intercepcion(4, 6, 12, 8)
      5.0
    """

La función intercepcion debe pasar la prueba unitaria.

Escriba una función llamada es_par(n) que tome como argumento un entero y devuelva True si el argumento es un número par y False si es un non.

Agregue su propio código para la prueba unitaria de esta función.
Ahora escriba la función es_non(n) que devuelva True cuando n es non y False en caso contrario. Incluya el código para la prueba unitaria de esta función conforme la vaya escribiendo.

Finalmente, modifíquela para que use una llamada a es_par para determinar si su argumento es un entero non.
```
def es_factor(f, n):
    """
      >>> es_factor(3, 12)
      True
      >>> es_factor(5, 12)
      False
      >>> es_factor(7, 14)
      True
      >>> es_factor(2, 14)
      True
      >>> es_factor(7, 15)
      False
    """
```
Agregue el cuerpo a la función es_factor para hacer que pase la prueba unitaria.

def es_multiplo(m, n):
    """
      >>> es_multiplo(12, 3)
      True
      >>> es_multiplo(12, 4)
      True
      >>> es_multiplo(12, 5)
      False
      >>> es_multiplo(12, 6)
      True
      >>> es_multiplo(12, 7)
      False
    """

Agregue el cuerpo a la función es_multiplo para hacer que pase la prueba unitaria. ¿Puede encontrar una forma de usar la función es_factor en su definición de es_multiplo?

```
def f2c(t):
    """
      >>> f2c(212)
      100
      >>> f2c(32)
      0
      >>> f2c(-40)
      -40
      >>> f2c(36)
      2
      >>> f2c(37)
      3
      >>> f2c(38)
      3
      >>> f2c(39)
      4
    """
```
Escriba el cuerpo de la función f2c diseñada para devolver el valor entero más próximo a los grados Celsius para una temperatura dada en grados Fahrenheit. (pista: querría hacer uso de la función de biblioteca round. Intente mostrar el contenido de round.__doc__ en una terminal de Python y experimente con la sentencia round hasta que conozca con precisión cómo funciona.)

def c2f(t):
    """
      >>> c2f(0)
      32
      >>> c2f(100)
      212
      >>> c2f(-40)
      -40
      >>> c2f(12)
      54
      >>> c2f(18)
      64
      >>> c2f(-48)
      -54
    """

Agregue el cuerpo a la función c2f para convertir grados Celsius a grados Fahrenheit.

Navigation