2. Values, expressions and statements¶
2.1. Programs and data¶
We can restate our previous definition of a computer program colloquially:
A computer program is a set of instructions to tell a computer to do things to stuff.
We will be spending the rest of this book deepening and refining our understanding of exactly what kinds of things a computer can do. Your ability to program a computer effectively will depend in large part on your ability to understand these things well, so that you can express what you want to accomplish in a language the computer can execute.
Before we get to that, however, we need to talk about the stuff on which computers operate.
Computer programs operate on data. A single piece of data can be called a datum, but we will use the related term, value.
A value is one of the fundamental things — like a letter or a number —
that a program manipulates. The values we have seen so far are 4 (the
result when we added 2 + 2), and "Hello, World!".
Values are grouped into different data types or classes.
Note
As mentioned last chapter in the What is a computer? section, at the
level of the hardware of the machine, all values are stored as a sequence
of bits, usually represented by the
digits 0 and 1. All computer data types, whether they be numbers,
text, images, sounds, or anything else, ultimately reduce to an
interpretation of these bit patterns by the computer.
Thankfully, high-level languages like Python give us flexible, high-level data types which abstract away the tedious details of all these bits and better fit our human brains.
4 is an integer, and "Hello, World!" is a string, so-called because
it contains a string of letters. You (and the interpreter) can identify strings
because they are enclosed in quotation marks.
If you are not sure what class a value falls into, Python has a function called type which can tell you.
>>> type("Hello, World!")
<class 'str'>
>>> type(17)
<class 'int'>
Not surprisingly, strings belong to the class str and integers belong to the class int. Less obviously, numbers with a point between their whole number and fractional parts belong to a class called float, because these numbers are represented in a format called floating-point. At this stage, you can treat the words class and type interchangeably. We’ll come back to a deeper understanding of what a class is in later chapters.
>>> type(3.2)
<class 'float'>
What about values like "17" and "3.2"? They look like numbers, but they
are in quotation marks like strings.
>>> type("17")
<class 'str'>
>>> type("3.2")
<class 'str'>
They are strings!
Don’t use commas in ints
When you type a large integer, you might be tempted to use commas between
groups of three digits, as in 42,000. This is not a legal integer in
Python, but it does mean something else, which is legal:
>>> 42000
42000
>>> 42,000
(42, 0)
Well, that’s not what we expected at all! Because of the comma, Python treats this as a pair of values in a tuple. So, remember not to put commas or spaces in your integers. Also revisit what we said in the previous chapter: formal languages are strict, the notation is concise, and even the smallest change might mean something quite different from what you intended.
2.2. Three ways to write strings¶
Strings in Python can be enclosed in either single quotes (') or double
quotes ("), or three of each (''' or """)
>>> type('This is a string.')
<class 'str'>
>>> type("And so is this.")
<class 'str'>
>>> type("""and this.""")
<class 'str'>
>>> type('''and even this...''')
<class 'str'>
Double quoted strings can contain single quotes inside them, as in "Bruce's
beard", and single quoted strings can have double quotes inside them, as in
'The knights who say "Ni!"'.
Strings enclosed with three occurrences of either quote symbol are called triple quoted strings. They can contain either single or double quotes:
>>> print('''"Oh no," she exclaimed, "Ben's bike is broken!"''')
"Oh no," she exclaimed, "Ben's bike is broken!"
>>>
Triple quoted strings can even span multiple lines:
>>> message = """This message will
... span several
... lines."""
>>> print(message)
This message will
span several
lines.
>>>
Python doesn’t care whether you use single or double quotes or the three-of-a-kind quotes to surround your strings: once it has parsed the text of your program or command, the way it stores the value is identical in all cases, and the surrounding quotes are not part of the value. But when the interpreter wants to display a string, it has to decide which quotes to use to make it look like a string.
>>> 'This is a string.'
'This is a string.'
>>> """And so is this."""
'And so is this.'
So the Python language designers chose to usually surround their strings by single quotes. What do think would happen if the string already contained single quotes? Try it for yourself and see.
2.3. String literals and escape sequences¶
A literal is a notation for representing a constant value of a built-in data type.
In string literals, most characters represent themselves, so if we
want the literal with letters s-t-r-i-n-g, we simply write 'string'.
But what if we want to represent the literal for a linefeed (what you get
when you press the <Enter> key on the keyboard), or a tab? These string
literals are not printable the way an s or a t is. To solve this
problem Python uses an
escape sequence to represent
these string literals.
There are several of these escape sequences that are helpful to know.
Escape Sequence |
Meaning |
|---|---|
|
Backslash ( |
|
Single quote ( |
|
Double quote ( |
|
Backspace |
|
Linefeed |
|
Tab |
\n is the most frequently used of these. The following example will
hopefully make what it does clear.
>>> print("Line 1\n\n\nLine 5")
Line 1
Line 5
>>>
2.4. Names and assignment statements¶
In order to write programs that do things to the stuff we now call values, we need a way to store our values in the memory of the computer and to name them for later retrieval.
We use Python’s assignment statement for just this purpose:
>>> message = "What's up, Doc?"
>>> n = 17
>>> pi = 3.14159
The example above makes three assignments. The first assigns the string value
"What's up, Doc?" to the name message. The second gives the integer
17 the name n, and the third assigns the floating-point number
3.14159 the name pi.
Assignment statements create names and associate these names with values. The values can then be retrieved from the computer’s memory by refering to the name associated with them.
>>> message
"What's up, Doc?"
>>> pi
3.14159
>>> n
17
>>> print(message)
What's up, Doc?
Names are also called variables, since the values to which they refer can change during the execution of the program. Variables also have types. Again, we can ask the interpreter what they are.
>>> type(message)
<class 'str'>
>>> type(n)
<class 'int'>
>>> type(pi)
<class 'float'>
The type of a variable is the type of the value it currently refers to.
A common way to represent variables on paper is to write the name of the variable with a line connecting it with its current value. This kind of figure is called an object diagram. It shows the state of the variables at a particular instant in time.
This diagram shows the result of executing the previous assignment statements:
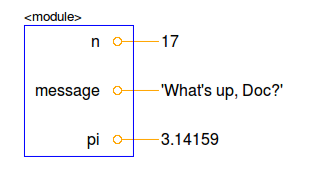
2.5. Variables are variable¶
We use variables in a program to “remember” things, like the current score at the football game. But variables are variable. This means they can change over time, just like the scoreboard at a football game. You can assign a value to a variable, and later assign a different value to the same variable.
Note
This is different from math. In math, if you give x the value 3, it cannot change to link to a different value half-way through your calculations!
>>> day = "Thursday"
>>> day
'Thursday'
>>> day = "Friday"
>>> day
'Friday'
>>> day = 21
>>> day
21
You’ll notice we changed the value of day three times, and on the third
assignment we even gave it a value that was of a different type.
Note
A great deal of programming is about having the computer remember things, like assigning a variable to the number of missed calls on your phone, and then arranging to update the variable when you miss another call.
In the Python shell, entering a name at the prompt causes the interpreter to
look up the value associated with the name (or return an error message if the
name is not defined), and to display it. In a script, a defined name not in a
print function call does not display at all.
2.6. The assignment operator is not an equal sign!¶
The semantics of the assignment statement can be confusing to beginning
programmers, especially since the assignment token, = can be easily
confused with the with equals (Python uses the token == for equals,
as we will see soon). It is not!
>>> n = 17
>>> n = n + 1
>>> n
18
The middle statement above would be impossible if = meant equals, since
n could never be equal to n + 1. This statement is perfectly legal
Python, however. The assignment statement links a name, on the left hand
side of the operator, with a value, on the right hand side.
The two ns in n = n + 1 have different meanings: the n on the
right is a memory look-up that is replaced by a value when the right hand side
is evaluated by the Python interpreter. It has to already exist or a name
error will result. The right hand side of the assignment statement is
evaluated first.
The n on the left is the name given to the new value computed on the right
hand side as it is stored in the computer’s memory. It does not have to exist
previously, since it will be added to the running program’s available names
if it isn’t there already.
Note
Names in Python exist within a context, called a namespace, which we will discuss later in the book.
The left hand side of the assignment statement does have to be a valid Python variable name. This is why you will get an error if you enter:
>>> 17 = n
Tip
When reading or writing code, say to yourself “n is assigned 17” or “n gets the value 17”. Don’t say “n equals 17”.
Note
In case you are wondering, a token is a character or string of characters that has syntactic meaning in a language. In Python operators, keywords, literals, and white space all form tokens in the language.
2.7. Variable names and keywords¶
Valid variable names in Python must conform to the following three simple rules:
They are an arbitrarily long sequence of letters and digits.
The sequence must begin with a letter.
In addtion to a..z, and A..Z, the underscore (
_) is a letter.
Although it is legal to use uppercase letters, by convention we don’t. If you
do, remember that case matters. day and Day would be different
variables.
The underscore character ( _) can appear in a name. It is often used in
names with multiple words, such as my_name or price_of_tea_in_china.
There are some situations in which names beginning with an underscore have special meaning, so a safe rule for beginners is to start all names with a letter other than the underscore.
If you give a variable an illegal name, you get a syntax error:
>>> 76trombones = "big parade"
SyntaxError: invalid syntax
>>> more$ = 1000000
SyntaxError: invalid syntax
>>> class = "Computer Science 101"
SyntaxError: invalid syntax
76trombones is illegal because it does not begin with a letter. more$
is illegal because it contains an illegal character, the dollar sign. But
what’s wrong with class?
It turns out that class is one of the Python keywords. Keywords define
the language’s syntax rules and structure, and they cannot be used as variable
names.
Python 3 has thirty-five keywords (and every now and again improvements to Python introduce or eliminate one or two):
and |
as |
assert |
async |
await |
break |
class |
continue |
def |
del |
elif |
else |
except |
finally |
for |
from |
global |
if |
import |
in |
is |
lambda |
nonlocal |
not |
or |
pass |
raise |
return |
try |
while |
with |
yield |
True |
False |
None |
You might want to keep this list handy. Actually, as will often be the case when learning to program with Python, when you aren’t sure about something, you can ask Python:
>>> import keyword
>>> keyword.kwlist
['False', 'None', 'True', 'and', 'as', 'assert', 'async', 'await',
'break', 'class', 'continue', 'def', 'del', 'elif', 'else', 'except',
'finally', 'for', 'from', 'global', 'if', 'import', 'in', 'is', 'lambda',
'nonlocal', 'not', 'or', 'pass', 'raise', 'return', 'try', 'while', 'with',
'yield']
The list of keywords, keyword.kwlist, comes to us, appropriately, in a
Python list.
If the interpreter complains about one of your variable names and you don’t know why, see if it is on this list.
Programmers generally choose names for their variables that are meaningful to the human readers of the program — they help the programmer document, or remember, what the variable is used for.
Caution
Beginners sometimes confuse meaningful to the human readers with
meaningful to the computer. So they’ll wrongly think that because
they’ve called some variable average or pi, it will somehow
automatically calculate an average, or automatically associate the variable
pi with the value 3.14159. No! The computer doesn’t attach semantic
meaning to your variable names. It is up to you to do that.
2.8. Statements and expressions¶
A statement is
an instruction that the Python interpreter can execute. We have seen two so
far, the assignment statement and the import statement. Some other kinds of
statements that we’ll see shortly are if statements, while statements,
and for statements. (There are other kinds too!)
When you type a statement on the command line, Python executes it. The interpreter does not display any results.
An expression is a combination of values, variables, operators, and calls to functions. If you type an expression at the Python prompt, the interpreter evaluates it and displays the result, which is always a value:
>>> 1 + 1
2
>>> len('hello')
5
In this example len is a built-in Python function that returns the number
of characters in a string. We’ve previously seen the print and the
type functions, so this is our third example of a function.
The evaluation of an expression produces a value, which is why expressions can appear on the right hand side of assignment statements. A value all by itself is a simple expression, and so is a variable.
>>> 17
17
>>> y = 3.14
>>> x = len('hello')
>>> x
5
>>> y
3.14
2.9. Operators and operands¶
Operators are special tokens that represent computations like addition, multiplication and division. The values the operator uses are called operands.
The following are all legal Python expressions whose meaning is more or less clear:
20 + 32 hour - 1 hour * 60 + minute minute / 60 5 ** 2
(5 + 9) * (15 - 7)
The tokens + and -, and the use of parenthesis for grouping, mean in
Python what they mean in mathematics. The asterisk (*) is the token for
multiplication, and ** is the token for exponentiation (raising a number to
a power).
>>> 2 ** 3
8
>>> 3 ** 2
9
When a variable name appears in the place of an operand, it is replaced with its value before the operation is performed.
Addition, subtraction, multiplication, and exponentiation all do what you expect.
Example: so let us convert 645 minutes into hours:
>>> minutes = 645
>>> hours = minutes / 60
>>> hours
10.75
Oops! In Python 3, the division operator / always yields a floating point
result. What we might have wanted to know was how many whole hours there
are, and how many minutes remain. Python gives us two different flavors of
the division operator. The second, called floor division uses the token
//. It always truncates its result down to the next smallest integer (to
the left on the number line).
>>> 7 / 4
1.75
>>> 7 // 4
1
>>> minutes = 645
>>> hours = minutes // 60
>>> hours
10
Take care that you choose the correct division operator. If you’re working with expressions where you need floating point values, use the division operator that does the division appropriately.
2.10. The modulus operator¶
The modulus operator works on integers (and integer expressions) and gives
the remainder when the first number is divided by the second. In Python, the
modulus operator is a percent sign (%). The syntax is the same as for other
operators:
>>> 7 // 3 # floor division operator
2
>>> 7 % 3
1
So 7 divided by 3 is 2 with a remainder of 1.
The modulus operator turns out to be surprisingly useful. For example, you can
check whether one number is divisible by another – if x % y is zero, then
x is divisible by y.
Also, you can extract the right-most digit or digits from a number. For
example, x % 10 yields the right-most digit of x (in base 10).
Similarly x % 100 yields the last two digits.
It is also extremely useful for doing conversions, say from seconds, to hours, minutes and seconds. So let’s write a program to ask the user to enter some seconds, and we’ll convert them into hours, minutes, and remaining seconds.
total_secs = int(input("How many seconds, in total? "))
hours = total_secs // 3600
secs_still_remaining = total_secs % 3600
minutes = secs_still_remaining // 60
secs_finally_remaining = secs_still_remaining % 60
print(hours, ' hrs ', minutes, ' mins ', secs_finally_remaining, ' secs')
2.11. Order of operations¶
When more than one operator appears in an expression, the order of evaluation depends on the rules of precedence. Python follows the same precedence rules for its mathematical operators that mathematics does. The acronym PEMDAS is a useful way to remember the order of operations:
Parentheses have the highest precedence and can be used to force an expression to evaluate in the order you want. Since expressions in parentheses are evaluated first,
2 * (3-1)is 4, and(1+1)**(5-2)is 8. You can also use parentheses to make an expression easier to read, as in(minute * 100) / 60, even though it doesn’t change the result.Exponentiation has the next highest precedence, so
2**1+1is 3 and not 4, and3*1**3is 3 and not 27.Multiplication and both Division operators have the same precedence, which is higher than Addition and Subtraction, which also have the same precedence. So
2*3-1yields 5 rather than 4, and5-2*2is 1, not 6. #. Operators with the same precedence are evaluated from left-to-right. In algebra we say they are left-associative. So in the expression6-3+2, the subtraction happens first, yielding 3. We then add 2 to get the result 5. If the operations had been evaluated from right to left, the result would have been6-(3+2), which is 1. (The acronym PEDMAS could mislead you to thinking that division has higher precedence than multiplication, and addition is done ahead of subtraction - don’t be misled. Subtraction and addition are at the same precedence, and the left-to-right rule applies.)
Note
Due to some historical quirk, an exception to the left-to-right left-associative rule is the exponentiation operator **, so a useful hint is to always use parentheses to force exactly the order you want when exponentiation is involved:
>>> 2 ** 3 ** 2 # the right-most ** operator gets done first!
512
>>> (2 ** 3) ** 2 # use parentheses to force the order you want!
64
The immediate mode command prompt of Python is great for exploring and experimenting with expressions like this.
2.12. Operations on strings¶
In general, you cannot perform mathematical operations on strings, even if the
strings look like numbers. The following are illegal (assuming that message
has type string):
message - 1 "Hello" / 123 message * "Hello" "15" + 2
Interestingly, the + operator does work with strings, but for strings, the
+ operator represents concatenation, not addition. Concatenation means
joining the two operands by linking them end-to-end. For example:
fruit = "banana"
baked_good = " nut bread"
print(fruit + baked_good)
The output of this program is banana nut bread. The space before the word
nut is part of the string, and is necessary to produce the space between
the concatenated strings.
The * operator also works on strings; it performs repetition. For example,
'Fun' * 3 is 'FunFunFun'. One of the operands has to be a string; the
other has to be an integer.
On one hand, this interpretation of + and * makes sense by analogy with
addition and multiplication. Just as 4 * 3 is equivalent to 4 + 4 + 4,
we expect "Fun" * 3 to be the same as "Fun" + "Fun" + "Fun", and it is.
On the other hand, there is a significant way in which string concatenation and
repetition are different from integer addition and multiplication. Can you
think of a property that addition and multiplication have that string
concatenation and repetition do not?
2.13. Formatted string literals¶
Python supports creating f-strings that
enable adding variables and expressions inside a string which are then
evaluated before the string is rendered. Just put an f or F in
front of the string:
name = "Susmita"
print(f"Hello, {name}, great to meet you!")
The example above will print Hello, Susmita, great to meet you!.
2.14. Type converter functions¶
Here we’ll look at three more Python functions, int, float and str,
which will (attempt to) convert their arguments into types int, float
and str respectively. We call these type converter functions.
The int function can take a floating point number or a string, and turn it
into an int. For floating point numbers, it discards the fractional portion
of the number - a process we call truncation towards zero on the number line.
Let us see this in action:
>>> int(3.14)
3
>>> int(3.9999) # This doesn't round to the closest int!
3
>>> int(3.0)
3
>>> int(-3.999) # Note that the result is closer to zero
-3
>>> int(minutes/60)
10
>>> int("2345") # parse a string to produce an int
2345
>>> int(17) # int even works if its argument is already an int
17
>>> int("23 bottles")
Traceback (most recent call last):
File "<interactive input>", line 1, in <module>
ValueError: invalid literal for int() with base 10: '23 bottles'
The last case shows that a string has to be a syntactically legal number, otherwise you’ll get one of those pesky runtime errors.
The type converter float can turn an integer, a float, or a syntactically
legal string into a float.
>>> float(17)
17.0
>>> float("123.45")
123.45
The type converter str turns its argument into a string:
>>> str(17)
'17'
>>> str(123.45)
'123.45'
2.15. Input¶
There is a built-in function in Python for getting input from the user:
name = input("Please enter your name: ")
The user of the program can enter the name and press return. When this
happens the text that has been entered is returned from the input function,
and in this case assigned to the variable name.
The string value inside the parentheses is called a prompt and contains a message which will be displayed to the user when the statement is executed to prompt their response.
When a key is pressed on a keyboard a single character is sent to a
keyboard buffer inside
the computer. When the
enter key is pressed, the
sequence of characters inside the keyboard buffer in the order in which they
were received are returned by the input function as a single string
value.
Even if you asked the user to enter their age, you would get back a string like
"17". It would be your job, as the programmer, to convert that string into
a int or a float, using the int or float converter functions we saw
in the previous section, which leads us to …
2.16. Composition¶
So far, we have looked at the elements of a program — variables, expressions, statements, and function calls — in isolation, without talking about how to combine them.
One of the most useful features of programming languages is their ability to take small building blocks and compose them into larger chunks.
For example, we know how to get the user to enter some input, we know how to convert the string we get into a float, we know how to write a complex expression, and we know how to print values. Let’s put these together in a small four-step program that asks the user to input a value for the radius of a circle, and then computes the area of the circle from the formula
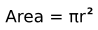
Firstly, we’ll do the four steps one at a time:
response = input("What is your radius? ")
r = float(response)
area = 3.14159 * r ** 2
print("The area is ", area)
Now let’s compose the first two lines into a single line of code, and compose the second two lines into another line of code.
r = float(input("What is your radius? "))
print("The area is ", 3.14159 * r ** 2)
If we really wanted to be tricky, we could write it all in one statement:
print("The area is ", 3.14159 * float(input("What is your radius? ")) ** 2)
Such compact code may not be most understandable for humans, but it does illustrate how we can compose bigger chunks from our building blocks.
If you’re ever in doubt about whether to compose code or fragment it into smaller steps, try to make it as simple as you can for the human reader to follow.
2.17. More about the print function¶
At the end of the previous chapter, you learned that the print function can take a series of arguments, seperated by commas, and that it prints a string with each argument in order seperated by a space.
In the example in the previous section of this chapter, you may have noticed that the arguments don’t have to be strings.
>>> print("I am", 12 + 9, "years old.")
I am 21 years old.
>>>
By default, print uses a single space as a seperator and a \n as a
terminator (at the end of the string). Both of these defaults can be
overridden.
>>> print('a', 'b', 'c', 'd')
a b c d
>>> print('a', 'b', 'c', 'd', sep='##', end='!!')
a##b##c##d!!>>>
You will explore these new features of the print function in the exercises.
2.18. Glossary¶
- assignment statement¶
A statement that assigns a value to a name (variable). To the left of the assignment operator,
=, is a name. To the right of the assignment token is an expression which is evaluated by the Python interpreter and then assigned to the name. The difference between the left and right hand sides of the assignment statement is often confusing to new programmers. In the following assignment:n = n + 1
nplays a very different role on each side of the=. On the right it is a value and makes up part of the expression which will be evaluated by the Python interpreter before assigning it to the name on the left.- assignment token¶
=is Python’s assignment token, which should not be confused with the mathematical comparison operator using the same symbol.- composition¶
The ability to combine simple expressions and statements into compound statements and expressions in order to represent complex computations concisely.
- concatenate¶
To join two strings end-to-end.
- data type¶
A set of values. The type of a value determines how it can be used in expressions. So far, the types you have seen are integers (
int), floating-point numbers (float), and strings (str).- escape sequence¶
A sequence of characters starting with the escape character (
\) used to represent string literals such as linefeeds and tabs.- evaluate¶
To simplify an expression by performing the operations in order to yield a single value.
- expression¶
A combination of variables, operators, and values that represents a single result value.
- float¶
A Python data type which stores floating-point numbers. Floating-point numbers are stored internally in two parts: a base and an exponent. When printed in the standard format, they look like decimal numbers. Beware of rounding errors when you use
floats, and remember that they are only approximate values.- int¶
A Python data type that holds positive and negative whole numbers.
- floor division¶
An operation that divides one integer by another and yields an integer. Floor division yields the next lower integer from the division of two integers.
- keyword¶
A reserved word that is used by the compiler to parse program; you cannot use keywords like
if,def, andwhileas variable names.- literal¶
A notation for representing for representing a constant value of one of Python’s built-in types.
\n, for example, is a literal representing the newline character.- modulus operator¶
An operator, denoted with a percent sign (
%), that works on integers and yields the remainder when one number is divided by another.- object diagram¶
A graphical representation of a set of variables (objects) and the values to which they refer, taken at a particular instant during the program’s execution.
- operand¶
One of the values on which an operator operates.
- operator¶
A special symbol that represents a simple computation like addition, multiplication, or string concatenation.
- rules of precedence¶
The set of rules governing the order in which expressions involving multiple operators and operands are evaluated.
- statement¶
An instruction that the Python interpreter can execute. So far we have only seen the assignment statement, but we will soon meet the
importstatement and theforstatement.- str¶
A Python data type that holds a string of characters.
- tripple quoted strings¶
A string enclosed by either
"""or'''. Tripple quoted strings can span several lines.- value¶
A number, string, or any of the other things that can be stored in a variable or computed in an expression.
- variable¶
A name that refers to a value.
- variable name¶
A name given to a variable. Variable names in Python consist of a sequence of letters (a..z, A..Z, and _) and digits (0..9) that begins with a letter. In best programming practice, variable names should be chosen so that they describe their use in the program, making the program self documenting.