6. Iteration¶

6.1. Multiple assignment¶

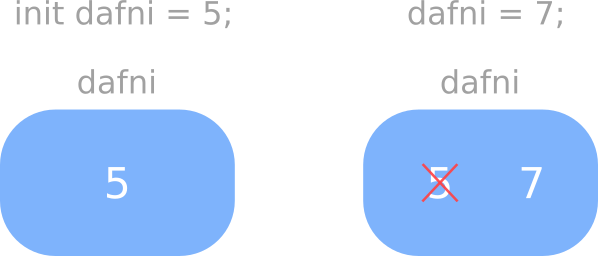
We haven’t said much about it, but it is legal in C++ to make more than one assignment to the same variable. The effect of the second assignment is to replace the value of the variable with a new value.

int nana = 5;
cout << nana;
nana = 7;
cout << nana << endl;

The output of this of this program is 57, because the first time we print nana her value is 5, and the second time her value is 7.

This kind of multiple assignment is the reason we described a variable as a container for values. When you assign a value to a variable, you change the contents of the container, as shown in the figure:

When there are multiple assignments to a variable, it is especially important to distinguish between an assignment statement and a statement of equality. Because C++ uses the = symbol for assignment, it is tempting to interpret a statement like a = b as a statement of equality. It is not!

First of all, equality is commutative, and assignment is not. For example, in mathematics if a = 7 then 7 = a. But in C++ the statement a = 7; is legal, and 7 = a; is not.

Furthermore, in mathematics, a statement of equality is true for all time. If a = b now, then a will always equal b. In C++, an assignment statement can make two variables equal, but they don’t have to stay that way!

int a = 5;
int b = a;      // a and b are now equal
a = 3;          // a and b are no longer equal

The third line changes the value of a but it does not change the value of b, and so they are no longer equal. In some other programming languages an alternate symbol is used for assignment, such as <- or :=, in order to avoid confusion.

Although multiple assignment is frequently useful, you should use it with caution. If the values of variables are changing constantly in different parts of the program, it can make the code difficult to read and debug.

6.2. Iteration¶

On of the things computers are often used for is the automation of repetitive tasks. Repeating identical or similar tasks without making errors is something that computers do extremely well and people do poorly.

We have seen programs that use recursion to perform repetition, such as nLines and countdown. The repetition examples in this chapter use iteration, and C++ provides several language features that make it easier to write iterative programs.

6.3. The `while` statement¶

Using a while statement, we can rewrite countdown:

void countdown(int n)
{
    while (n > 0) {
        cout << n << endl;
        n = n - 1;
    }
    cout << "Blastoff!" << endl;
}

You can almost read a while statement as if it were English. What this example says is, “While n is greater than zero, continue displaying the value of n and then reducing the value of n by 1. When you get to zero, output the word ‘Blastoff!’”

More formally, the flow of execution for a while statement is as follows:

Evaluate the condition in parentheses, yielding true or false.
If the condition is false, exit the while statement and continue execution at the next statement.
If the condition is true, execute each of the statements between the curly braces, and then go back to step 1.

This type of flow is called a loop because the third step loops back around to the top. Notice that if the condition is false the first time through the loop, the statements inside the loop never executed. The statements inside the loop are called the body of the loop.

The body of the loop should change the value of one or more variables so that, eventually, the condition becomes false and the loop terminates. Otherwise the loop will repeat forever, which is called an infinite loop. An endless source of amusement for computer scientists is the observation that the directions on shampoo, “Lather, rinse, repeat,” are an infinite loop.

In the case of countdown, we can prove that the loop will terminate because we know that the value of n is finite, and we can see that the value of n gets smaller each time through the loop (each iteration), so eventually we have to get to zero. In other cases it is not so easy to tell:

void sequence(int n)
{
   while (n != 1) {
       cout << n << endl;
       if (n%2 == 0) {      // n is even
           n = n / 2;
       } else {             // n is odd
           n = n * 3 + 1;
       }
   }
}

The condition for this loop is n != 1, so the loop will continue until n is 1, which will make the condition false.

At each iteration, the program outputs the value of n and then checks whether is is even or odd. If it is even, the value of n is divided by two. If it is odd, the value is replaced by \(3n + 1\). For example, if the starting value (the argument passed to sequence) is 3, the resulting sequence is 3, 10, 5, 16, 8, 4, 2, 1.

Since n sometimes increases and sometimes decreases, there is no obvious proof that n will ever reach 1, or that the program will terminate. For some particular values of n, we can prove termination. For example, if the starting value is a power of two, then the value of n will be even every time through the loop, until we get to 1.

Particular values aside, the interesting question is whether we can prove that this program terminates for all values of n. So far, no one has been able to prove or disprove it!

6.4. `for` loops¶

A common pattern when using a loop is to start by initializing a variable; then have a test, or condition, that depends on that variable; and inside the loop do something to that variable, like increment it.

This type of loop is so common that there is an alternative loop statement, called for, that expresses it more concisely. The general syntax looks like this:

for (INITIALIZER; CONDITION; INCREMENTOR) {
    BODY
}

This statement is exactly equivalent to

INITIALIZER
while (CONDITION) {
    BODY
    INCREMENTOR
}

except that is is more concise and, since it puts all the loop related statements in one place, it is easier to read. For example:

for (int i = 0; i < 4; i++) {
    cout << count[i] << endl;
}

is equivalent to

int i = 0;
while (i < 4) {
    cout << count[i] << endl;
    i++;
}

Notice that it is legal to declare a variable inside a for statement. This syntax is convenient, but you should be aware that a variable declared inside a loop only exists inside the loop. If you try to refer to i later, you will get a compiler error.

6.5. `do-while` loops¶

The last looping statement we will look at is the do-while loop, which has the general syntax:

do {
    BODY
} (CONDITION);

Like the while statement, the do-while statement is sometimes referred to as an indefinite loop, since the number of times the loop body will execute may not be clear. This is in contrast to the for statement, referred to as a definite loop, since the number of loop executions can usually be determined by the three statements in the parenthesis immediately following the for.

A do-while loop is used when you know you want the loop body to execute at least once. Here is a math quiz program that keeps asking the user multiplication until they get one wrong:

#include <time.h>
#include <stdlib.h>
#include <iostream>
using namespace std;

int main() {
    srand(time(NULL));
    unsigned int m1, m2, prod, num_correct = 0;
    bool correct;

    cout << "\nOkay, let's see how many multiplication questions in ";
    cout << "a row you can get right." << endl;
    cout << "I'll keep asking you questions until you get one wrong." << endl;
    cout << "I'll also keep count for you. Ready? Let's go...\n" << endl;
    do {
        m1 = rand() % 10; 
        m2 = rand() % 10; 
        cout << "What is " << m1 << " times " << m2 << "? ";
        cin >> prod;
        correct = prod == m1 * m2;
        if (correct) {
            cout << "That's right. Well done!" << endl;
            num_correct++;
        }
        else
            cout << "No, the correct answer is " << m1 * m2 << "." << endl;
    } while (correct);
    cout << "You got " << num_correct << " questions right in a row.";
    cout << " Nice job!" << endl;
    return 0;
}

6.6. Tables¶

One of the things that loops are good for is generating tabular data. For example, before computers were reaadily available, people had to calculate logarithms, sines and cosines, and other common mathematical functions by hand. To make that easier, there were books containing long tables where you could find the values of various functions. Creating these tables was slow and boring, and the result tended to be full of errors.

Note

The book and movie Hidden Figures traces the history of some of the African American women who worked as computers at NASA during the early days of space program. They were doing just these kinds of calculations by hand at the time digital computers were first introduced. Indeed, the need to greatly speed up calculations like these was one of the prime motivating forces in the development of digital computers.

When computers appeared on the scene, one of the intial reactions was, “This is great! We can use computers to generate the tables, so there will be no errors.” That turned out to be true (mostly), but shortsighted. Soon thereafter computers and calculators were so pervasive that the tables became obsolete.

Well, almost. It turns out that for some operations, computers use tables of values to get an approximate answer, and then perform computations to improve the approximation.

Note

In some cases, there have been errors in the underlying tables, most famously in the table the orginal Intel Pentium used to perform floating-point division.

Although a “log table” is not as useful as it once was, it still makes a good example of iteration. The following program outputs a sequence of values in the left column and their logorithms in the right column:

for (int x = 1; x < 10; x++)
    cout << x << "\t" << log(x) << "\n";

The sequence \t represents a tab character. The sequence \n represents a newline character. These sequences can be included anywhere in a string, although in the above example they make up the whole string.

A tab character causes the cursor to shift to the right until it reaches one of the tab stops, which are normally every eight characters. As we will see in a minute, tabs are useful for making columns of text line up.

A newline character has exactly the same effect as endl; it causes the cursor to move on to the next line. Usually if a newline character appears by itself, we will use endl, but if it appears as part of a larger string, we’ll use \n.

The output of this program is:

If these values see odd, remember that the log function uses base e. Since powers of two are so important in computer science, we often want to find logorithms with respect to base 2. To do that, we can use the following formula:

\[log_2 x = \frac{log_e x}{log_e 2}\]

Changing the output statement to

cout << x << "\t" << log(x) / log(2.0) << endl;

yields

We can see that 1, 2, 4, and 8 are powers of two, because their logarithms base 2 are round numbers. If we wanted to find the logarithms of other powers of two, we could modify the program like this:

for (int x; x < 130; x *= 2)
    cout << x << "\t" << log(x) / log(2.0) << endl;

Now instead of adding something to x each time through the loop, which yields an arithmetic sequence, we multiply x by something, yielding a geometric sequence. The result is:

Because we are using tab characters between the columns, the position of the second column does not depend on the number of digits in the first column.

6.7. Two-dimensional tables¶

A two-dimensional table is a table where you choose a row and a column and read the value at the intersection. A multiplication table is a good example. Let’s say you wanted to print a multiplication table for the values from 1 to 6.

A good way to start is to write a simple loop that prints the multiples of 2, all on one line.

for (int i = 1; i <= 6; i++)
    cout << 2 * i << "   ";
cout << endl;

The first line initializes a variable named i, which is going to act as a counter or loop variable. As the loop executes, the value of i increases from 1 to 6, and then when i is 7, the loop terminates. Each time through the loop, we print the value of 2 * i followed by three spaces. By omitting the endl from the first output statement, we get all the output on a single line.

The output of this program is:

2   4   6   8   10   12

So far, so good. The next step is to encapsulate and generalize.

6.8. Encapsulation and generalization¶

Encapsulation usually means taking a piece of code and wrapping it up in a function, allowing you to take advantage of all the things that functions are good for. We have seen two examples of encapsulation already, when we wrote print_parity in Alternative execution and is_single_digit in Boolean functions.

Generalization means taking something specific, like printing multiples of 2, and making it more general, like printing the multiples of any integer.

Here’s a function that encapsulates the loop from the previous section and generalizes it to print multiples of n.

void print_multiples(int n)
{
    for (int i = 1; i <= 6; i++)
        cout << n * i << "   ";
    cout << endl;
}

To encapsulate, all we had to do was add the first line, which declares the name, parameter, and return type, thus wrapping our code in a function. To generalize, all we had to do was replace the value 2 with the parameter n.

If we call this function with the argument 2, we get the same output as before. With argument 3, the output is:

3   6   9   12   15   18

and with argument 4, the output is:

4   8   12   16   20   24

By now you can probably guess how we are going to print a multiplication table: we’ll call print_multiples repeatedly with different arguments. In fact, we are going to use another loop to iterate through the rows.

for (int i = 1; i <= 6; i++)
    print_multiples(i);

First of all, notice how similar this loop is to the one inside print_multiples. All we did was replace the print statement with a function call.

The output of the program is

 2   3   4   5   6
 4   6   8   10   12
 6   9   12   15   18
 8   12   16   20   24
 10   15   20   25   30
 12   18   24   30   36

which is a (slightly sloppy) multiplication table. If the sloppiness bothers you, try replacing the spaces between the columns with tab characters and see what you get.

6.9. Functions¶

In the last section we mentioned “all the things functions are good for.” About this time, you might be wondering what exactly those things are. Here are some of the reasons functions are useful:

By giving a name to a sequence of statements, you make your program easier to read and debug.
Dividing a long program into functions allows you to separate parts of the program, debug them in isolation, and then compose them into a whole.
Functions facilitate both recursion and iteration.
Well-designed functions are often useful for many programs. Once you write and debug one, you can reuse it.

6.10. More encapsulation¶

To demonstrate encapsulation again, we’ll take the code from the previous section and wrap it up in a function:

void print_mult_table()
{
    for (int i = 1; i <= 6; i++)
        print_multiples(i);
}

The process we are demonstrating is a common development plan. You develop code gradually by adding lines to main or someplace else, and then when you get it working, you extract it and wrap it up in a function.

The reason this is useful is that you sometimes don’t know when you start writing exactly how to divide the program into functions. This approach lets you design as you go along.

6.11. Local variables¶

About this time, you might be wondering how we can use the same variable i in both print_multiples and print_mult_table. Didn’t we say that you can only declare a variable once? And doesn’t it cause problems when one of the functions changes the value of a variable?

The answer to both questions is “no,” because the i in print_multiples and the i in print_mult_table are not the same variable. They have the same name, but the do not refer to the same storage location, and changing the value of one of them has no effect on the other.

Remember that variables that are declared inside a function definition are local. You cannot access a local variable from outside its “home” function, and you are free to have multiple variables with the same name, as long as they are not in the same function.

Note

This is an example of the concept in computing called a namespace, about which we will have more to say later.

The stack diagram for this program shows clearly that the two variables named i are not the same storage location. They can have different values, and changing one does not affect the other.

Notice that the value of the parameter n in print_multiples has to be the same as the value of i in print_mult_table. On the other hand, the value of i in print_multiples goes from 1 up to n. In the diagram it happens to be 3. The next time through the loop it will be 4.

It is often a good idea to use different variable names in different functions, to avoid confusion, but there are good reasons to reuse names. For example, it is common to use the names i, j, and k as loop variables. If you avoid using them in one function just because you used them somewhere else, you will probably the program harder to read.

6.12. More generalization¶

As another example of generalization, imagine you wanted a program that would print a multiplication table of any size, not just the 6x6 table. You could add a parameter to print_mult_table:

void print_mult_table(int high)
{
    for (int i = 1; i <= high; i++)
        print_multiples(i);
}

We replaced the value 6 with the parameter high. If we call print_mult_table with the argument 7, we get

 2   3   4   5   6
 4   6   8   10   12
 6   9   12   15   18
 8   12   16   20   24
 10   15   20   25   30
 12   18   24   30   36
 14   21   28   35   42

which is fine, except that we probably want the table to be square (same number of rows and columns), which means we have to add another parameter to print_multiples, to specify how many columns the table should have.

Just to be annoying, we will also call this parameter high, demonstrating that different functions can have parameters with the same name (just like local variables):

void print_multiples(int n, int high)
{
    for (int i = 1; i <= high; i++)
        cout << n * i << "   ";
    cout << endl;
}

void print_mult_table(int high)
{
    for (int i = 1; i <= high; i++)
        print_multiples(i, high);
}

Notice that when we added a new parameter, we had to change the first line of the function (the interface or prototype), and we also had to change the place where the function is called in print_mult_table. As expected, this program generates a square 7x7 table:

 2   3   4   5   6   7
 4   6   8   10   12   14
 6   9   12   15   18   21
 8   12   16   20   24   28
 10   15   20   25   30   35
 12   18   24   30   36   42
 14   21   28   35   42   49

When you generalize a function appropriately, you often find that the resulting program has capbilities that you did not intend. For example, you might notice that the multiplication table is symmetric, because \(ab = ba\), so all the entries in the table appear twice. You could have saved ink by printing only half the table. To do that, you only have to change one line of print_mult_table. Change

print_multiples(i, high);

print_multiples(i, i);

and you get

1
 4
 6   9
 8   12   16
 10   15   20   25
 12   18   24   30   36
 14   21   28   35   42   49

We’ll leave it up to you to figure out how it works.

6.13. Control flow within loops¶

We were introducted to the break statement back in The switch statement section; break can also be used to exit from the middle of the body of a loop.

Provide good example here...

Sometimes what is desired is not to leave the loop, but to halt execution of the current interation and start the next one. C++ provides the continue statement for just this purpose.

Provide good example here...

6.14. Glossary¶

development plan¶: A process for developing a program. In this chapter, we demonstrated a style of development based on starting with code to do simple, specific thingss, and then encapsulating and generalizing.
encapsulate¶: To divide a large complex program into components (like functions) and isolate the components from each other (for example, but using local variables).
generalize¶: To replace something unnecessarily specific (like a constant value) with something appropriately general (like a variable or parameter). Generalization makes code more versatile, more likely to be reused, and sometimes even easier to write.
infinite loop¶: A loop whose condition is always true.
local variable¶: A variable that is declared inside a function and that exists only within that function. Local variables cannot be accessed from outside their home functions, and do not interfere with any other functions.
loop¶: A statement that executes repeatedly while a condition is true or until some condition is satisfied.
loop body¶: The sequence of statements inside the loop.
tab¶: A special character, written as \t in C++, that causes the cursor to move to the next tab stop on the current line.

6. Iteration¶

6.1. Multiple assignment¶

6.2. Iteration¶

6.3. The while statement¶

6.4. for loops¶

6.5. do-while loops¶

6.6. Tables¶

6.7. Two-dimensional tables¶

6.8. Encapsulation and generalization¶

6.9. Functions¶

6.10. More encapsulation¶

6.11. Local variables¶

6.12. More generalization¶

6.13. Control flow within loops¶

6.14. Glossary¶

6.15. Exercises¶

6.3. The `while` statement¶

6.4. `for` loops¶

6.5. `do-while` loops¶